Retrieving Tropospheric Humidity from ATMS
Isaac Moradi, CICS-MD, ESSIC, University of Maryland
Atmospheric water vapor significantly contributes to the Earth's radiation budget and is a critical variable for climate studies. It is the dominant natural greenhouse gas and the largest known feedback mechanisms for amplifying global warming. Tropospheric humidity both directly and indirectly affects the hydrological cycle as well as strongly contributes to the water vapor feedback, especially in mid-upper troposphere, owing to the low temperatures at those altitudes. The concentration of water vapor in the upper troposphere is projected to double by the end of the century. However the fractional increase in upper tropospheric water vapor will be roughly three times as large as that for the lower troposphere, even though the relative humidity remains (nearly) constant at all levels (Held et al., 2000, Minschwaner et al., 2004, Soden et al., 2005).
The importance of water vapor underscores the need for an accurate understanding of the changes in its distribution over space and time. Satellite and radiosonde data are the main sources that provide information about tropospheric humidity. Radiosonde data have higher vertical resolution but coarser temporal and spatial resolution than satellite data. In addition, previous studies, e.g. Moradi et al., 2013, Elliott et al., 1991, Miloshevich et al., 2001, show that radiosonde data are prone to several errors, including contamination, sensor design, calibration, and data processing, particularly in the dry and cold conditions of the middle to upper troposphere.
Satellite data have global coverage with fine spatial resolution and are operationally available every few hours. However, satellite retrievals provide layer averages and do not resolve finer vertical structures of the tropospheric humidity. In addition, satellite data are measured in terms of radiance or brightness temperature (Tb); therefore transformation algorithms are required to convert the satellite Tb's to geophysical variables such as water vapor.
A simple and computationally effective technique which is based on a logarithmic relation between layer averaged tropospheric humidity and satellite brightness temperatures (Figure 1) is presented that can be used to directly convert the Advanced Technology Microwave Sounder (ATMS) radiances into layer-averaged humidity.
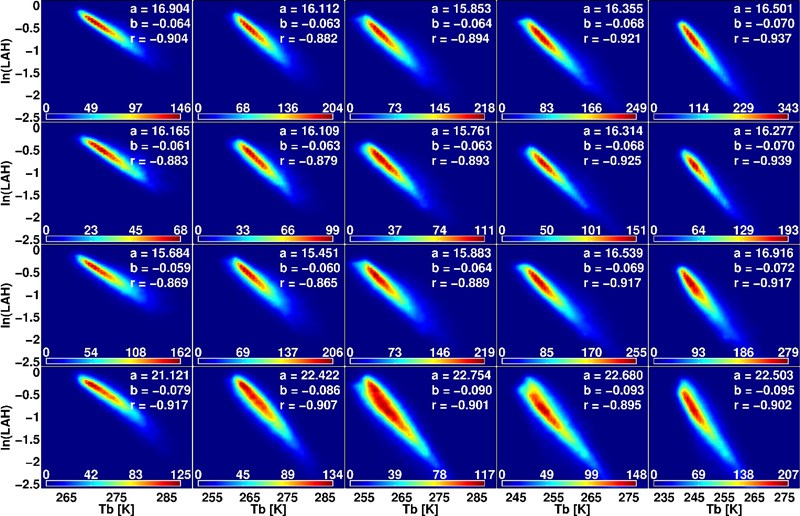
Figure 1: Jacobian weighted layer averaged humidity versus simulated satellite Tb's. The columns from left to right are for the ATMS Channels 18-22, respectively. ATMS Tb's and Jacobians were simulated using (first row) the combined dataset and the LBL model, (second row) the SeeBor dataset and the LBL model, (third row) the combined dataset and the fast model, and (fourth row) Tb's were simulated using the LBL model and combined dataset but the LAH values were calculated using the fixed Jacobians.
The empirical coefficients of this linear relation were calculated using different datasets as well as a fast and a line-by-line radiative transfer (RT) model. It was found that the coefficients do not significantly depend on the dataset or the RT model. This Tb to LAH transformation method can be applied to either original or limb corrected ATMS Tb's. In the former case, the coefficients are calculated as a function of earth incidence angle, and in the latter case, a method is presented to adjust the ATMS Tb's for the limb darkening effect then the same coefficients can be applied to all the ATMS Tb's from different beam positions. The algorithms were validated using both simulated and observed ATMS Tb's and the systematic difference between the estimated and calculated LAH values was lass than 10% in most cases. Overall, the method slightly underestimates LAH in moist conditions. Since there is a large interest in the LAH values averaged over a fixed layer, we also tested the transformation method using a fixed Jacobian for each channel. The bias generally increases when fixed Jacobians are used, but there is still a satisfactory agreement between estimated and calculated LAH values.
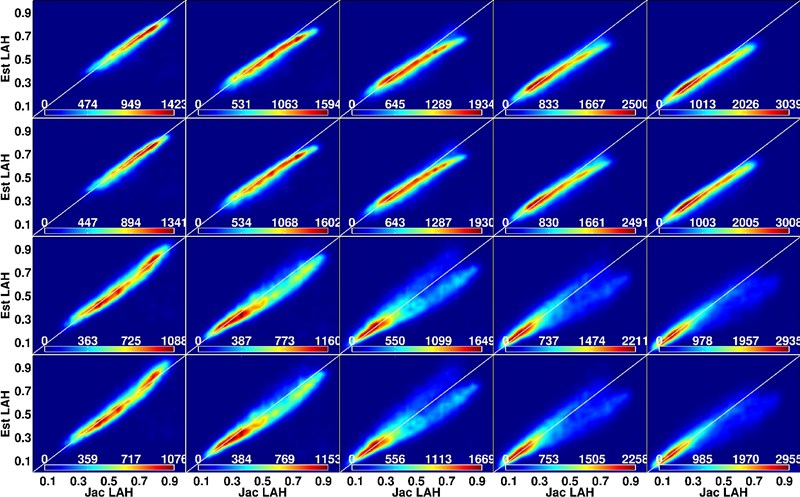
Figure 2: Estimated versus Jacobian weighted LAH values for the ARM radiosonde data. The ATMS brightness temperatures were simulated using the LBL model. The LAH values were calculated using the actual Jacobians for the first two rows and using fixed Jacobians for the last two rows: (first row) no-limb correction, (second row) limb-corrected, (third-row) no-limb correction, and (fourth row) limb-corrected.
« Back